7 ecuații care au schimbat lumea. Ce reprezintă fiecare dintre ele

Ecuațiile matematice oferă ferestre unice către lume. Ele dau sens realității și ne ajută să vedem lucruri care nu au fost observate anterior. Nu este surprinzător că noile evoluții în matematică au mers adesea mână în mână cu progresele în înțelegerea noastră a universului. Află care sunt cele mai cunoscute ecuații din istorie care au schimbat lumea.

Cele mai cunoscute ecuații care au schimbat lumea

Mediul încojurător nu l-am înțelege astfel dacă nu ar fi fost matematicienii care, de-a lungul timpului au dezvoltat ecuații cu care să ne poată permite depășirea barierelor. Iată care sunt cele mai cunoscute ecuații care au schimbat lumea.

Teorema lui Pitagora

Știri din lume

Dovada că Charlie Chaplin a fost ROMÂN! Cum a devenit prieten cu Ana Aslan

Știri din lume

10 locuri din Maramureș pe care trebuie să le vizitezi. Localnicii își respectă, cu sfințenie,...

Una dintre primele reguli trigonometrice majore pe care oamenii le învață la școală este relația dintre laturile unui triunghi dreptunghic: lungimea fiecăreia dintre cele două laturi mai scurte la pătrat și adunate împreună este egală cu lungimea celei mai lungi laturi la pătrat. Acesta este de obicei scris ca a^2 + b^2 = c^2 și este cunoscut de cel puțin 3.700 de ani, încă de pe vremea vechilor babilonieni.

Matematicianul grec Pitagora este creditat că a notat versiunea ecuației folosită astăzi, potrivit Universității din St. Andrews din Scoția. Odată cu găsirea utilizării în construcție, navigație, realizarea de hărți și alte procese importante, teorema lui Pitagora a ajutat la extinderea conceptului de numere.

În secolul al V-lea î.Hr., matematicianul Hippasus din Metapontum a observat că un triunghi dreptunghic isoscel ale cărui două laturi de bază au 1 unitate de lungime va avea o ipotenuză care este rădăcina pătrată a lui 2, care este un număr irațional. Pentru descoperirea sa, se spune că Hippasus a fost aruncat în mare.

F = ma și legea gravitației

Britanicul Sir Isaac Newton este creditat cu un număr mare de descoperiri zguduitoare. Printre acestea se numără a doua lege a mișcării, care afirmă că forța este egală cu masa unui obiect înmulțită cu accelerația sa, de obicei scrisă ca F = ma. O extindere a acestei legi, combinată cu celelalte observații ale lui Newton, l-au determinat, în 1687, să descrie ceea ce se numește acum legea gravitației universale.

Se scrie de obicei ca F = G (m1 * m2) / r^2, unde m1 și m2 sunt masele a două obiecte și r este distanța dintre ele. G este o constantă fundamentală a cărei valoare trebuie descoperită prin experimentare. Aceste concepte au fost folosite pentru a înțelege multe sisteme fizice de atunci, inclusiv mișcarea planetelor din sistemul solar și mijloacele de a călători între ele folosind rachete.

Ecuația undelor

Folosind legile relativ noi ale lui Newton, oamenii de știință din secolul al XVIII-lea au început să analizeze totul în jurul lor. În 1743, polimatul francez Jean-Baptiste le Rond d’Alembert a derivat o ecuație care descrie vibrațiile unei unde oscilante sau mișcarea unei unde, conform unei lucrări publicate în 2020 în revista Advances in Historical Studies. Ecuația poate fi scrisă astfel:

1/v^2 * ∂^2y/∂t^2= ∂^2y/∂x^2

În această ecuație, v este viteza unei unde, iar celelalte părți descriu deplasarea undei într-o direcție. Extinsă la două sau mai multe dimensiuni, ecuația undelor le permite cercetătorilor să prezică mișcarea apei, a undelor seismice și sonore și stă la baza unor lucruri precum ecuația Schrödinger a fizicii cuantice, care stă la baza multor gadget-uri moderne bazate pe computer.

Ecuațiile lui Fourier

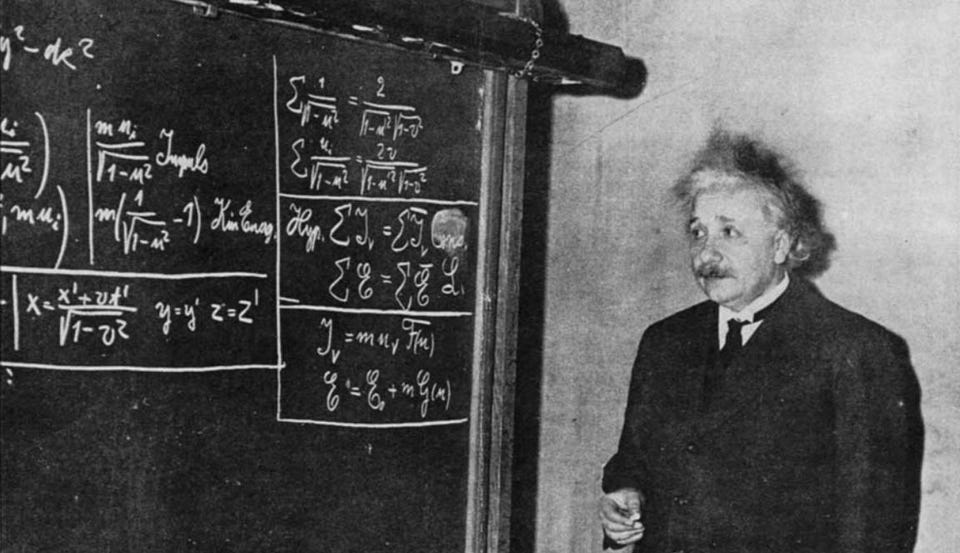
Chiar dacă nu ai auzit de baronul francez Jean-Baptiste Joseph Fourier, munca lui ți-a afectat viața într-o oarecare măsură. Asta pentru că ecuațiile matematice pe care le-a scris în 1822 au permis cercetătorilor să descompună date complexe și dezordonate în combinații de unde simple care sunt mult mai ușor de analizat. Ecuația lui Fourier, așa cum se știe, a fost o noțiune radicală în timpul său, mulți oameni de știință refuzând să creadă că sistemele complicate ar putea fi reduse la o simplitate atât de elegantă, potrivit unui articol din Yale Scientific.

Ecuațiile lui Maxwell

Electricitatea și magnetismul erau încă concepte noi în anii 1800, când oamenii de știință au investigat cum să capteze și să valorifice aceste forțe ciudate. Omul de știință scoțian James Clerk Maxwell ne-a îmbunătățit considerabil înțelegerea ambelor fenomene în 1864, când a publicat o listă de 20 de ecuații care descriu modul în care electricitatea și magnetismul funcționau și erau interconectate. Mai târziu perfecționate la patru, ecuațiile lui Maxwell sunt acum predate studenților de la fizică din primul an de la facultate și oferă o bază pentru tot ce este electronic în lumea noastră tehnologică modernă.

E = mc^2

Nicio listă de ecuații transformaționale nu ar putea fi completă fără cea mai faimoasă ecuație dintre toate. Afirmată pentru prima dată de Albert Einstein în 1905, ca parte a teoriei sale revoluționare a relativității speciale, E = mc^2 a arătat că materia și energia sunt două aspecte ale unui singur lucru.

În ecuație, E reprezintă energie, m reprezintă masa și c este viteza constantă a luminii. Noțiunile conținute într-o afirmație atât de simplă sunt încă greu de înțeles pentru mulți oameni, dar fără E = mc^2, nu am înțelege cum au funcționat stelele sau universul sau nu am ști cum să construim acceleratoare de particule gigantice.

Ecuația informațională a lui Shannon

Majoritatea oamenilor sunt familiarizați cu 0-urile și 1-urile care alcătuiesc biții computerului. Dar acest concept critic nu ar fi devenit popular fără munca de pionierat a matematicianului și inginerului american Claude Shannon. Într-o lucrare importantă din 1948, Shannon a prezentat o ecuație care arată eficiența maximă la care ar putea fi transmisă informația, adesea dată ca C = B * 2log(1+S/N).

În formulă, C este capacitatea realizabilă a unui anumit canal de informare, B este lățimea de bandă a liniei, S este puterea medie a semnalului și N este puterea medie a zgomotului. În lucrarea din 1948, Shannon atribuie ideea bitului matematicianului John W. Tukey ca prescurtare pentru expresia „cifră binară”.